I’ve been interested in different ways of tiling the plane ever since I read a 1977 Scientific American article on different periodic tilings using convex pentagons and hexagons. There are nonperiodic tilings too, such as the famous Penrose tiles where two different shapes of tile create a mosaic that extends infinitely in all directions but never exactly repeats. Penrose tiles are an example of a substitution tiling, generated by repeatedly substituting every tile with a set of smaller tiles. There are many other examples including a few intriguing ones where the tiles are rotated into infinitely many orientations, the most famous of these being the pinwheel tiling. I’ve discovered another with infinite orientations, and the added intriguing property of having tiles in an infinite range of sizes.
To begin, I must explain that I was playing with a tribonacci rectangle and looking for an interesting way to tile it. Exactly why I was doing that is a rabbit hole we won’t go down. The tribonacci rectangle is related to the tribonacci sequence (0, 1, 1, 2, 4, 7, 13, 24, 44…) in the same way that the golden rectangle is related to the fibonacci sequence (1, 1, 2, 3, 5, 8, 13, 21…).
So, if I divide the tribonacci rectangle into two triangles, I can create substitution rules as follows:

Each substitution creates three sizes of triangle, irrationally proportioned relative to each other, plus a trapezoid. Here’s the result, in which I’ve shaded some triangles depending on their “handedness”:

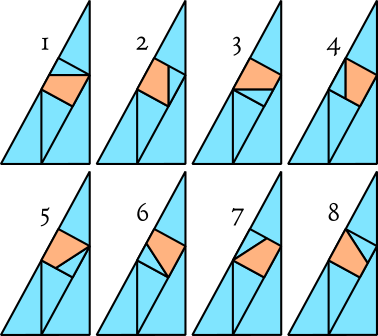
This can be made more interesting by modifying the first substitution rule:

The square that now appears in the centre of the substitution rule can be flipped and rotated into any of 8 orientations, yielding substitution rules for 8 different tilings. Tilings 1 to 4, in which the square is merely rotated, only yield a small set of tile orientations. But tilings 5 to 8, in which the square has also been reflected, all result in infinite tile orientations.
Here’s an example tiling for the fifth variant, above:

I really like how frequently edges meet each other, even across the boundary between the two original large triangles. This is despite all the “cuts” being at irrational proportions along each side.
Here’s another example, the 8th variant in the family:

